Una expresión algebraica es aquella en la que se utilizan o relacionan letras, números y signos de operaciones de suma, resta, multiplicación y división y también potencias, radicales y logaritmos.
Por ejemplo,
Suma de cuadrados: a2 + b2
Triple de un número menos doble de otro: 3x - 2y
Suma de varias potencias de un número: a4 + a3 + a2 + a
Multiplicación de radicales: 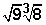
Si dos o más expresiones algebraicas están unidas con un signo más (+) o un signo menos (-) cada una recibe el nombre detérmino. Ahora, si dos o más expresiones algebraicas están unidas por una multiplicación cada una recibe el nombre de factor.
Veamos esto:
4ac es una expresión algebraica
(a + b) (a – b) es otra expresión algebraica
si las sumamos
4ac + (a + b)(a – b)
4ac pasa a ser el primer término y (a + b)(a – b) pasa a ser el segundo término.
Aquí vemos que el primer término es una multiplicación entre tres factores: el 4, una a y una c.
Y que el segundo término es una multiplicación entre dos factores: (a + b) por (a – b)
También debemos recordar que un término puede constar de las siguientes partes:
Una parte literal: representada por una o varias letras
Un coeficiente: valor que precede a la parte literal
Un exponente: que indica las veces que se multiplica por sí misma la parte literal .
Por ejemplo, en 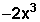
la x es la parte literal
el menos 2 es el coeficiente y
el 3 representa las veces que la parte literal se multiplica por sí misma (potencia).
Recordemos, además, que las expresiones algebraicas se clasifican, según su número de términos, en:
monomio, si tiene un solo término
binomio, si tien dos términos
trinomio si tiene tres, y, en general,
polinomio, si tiene más de dos.
Multiplicar expresiones algebraicas fraccionarias (racionales)
Entrando en materia, al comienzo hablamos de expresiones algebraicas racionales, que son aquellas en las cuales dos expresiones algebraicas forman una fracción (división, cociente o razón).
Por ejemplo:
Para resolver multiplicaciones con expresiones racionales (que involucren fracciones) debemos tener en cuenta lo siguiente:
- Toda fracción consta de numerador (el número de arriba) y denominador (el número de abajo).
- Para multiplicar fracciones se multiplica numerador por numerador y denominador por denominador.
- Respetar la regla de los signos para la multiplicación.
- Multiplicar entre sí los coeficientes numéricos y entre sí las letras iguales (la parte literal).
- Encontrar o visualizar los factores adecuados para realizar una factorización conveniente, que nos permita luego
- Simplificar o reducir las fracciones a su mínima expresión.
- Reordenar finalmente el numerador y el denominador respetando la secuencia de números y letras (a, b, c, etc.).
Para intentar una mayor comprensión, resolvamos los ejemplos:
Para intentar una mayor comprensión, resolvamos los ejemplos:
Ejemplo 1:
Resolvemos en único paréntesis que tenemos en la expresión:
Y la multiplicación nos queda así:
Multiplicamos los numeradores entre sí y los denominadores entres sí
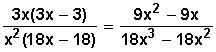
Factorizamos, para poder simplificar hasta donde sea posible:
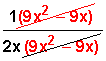
Simpliicamos, eliminando el binomio que se repite en el numerador y el denominador (en rojo), para quedar el resultado
Otra forma sería partiendo por factorizar el primer numerador (3x – 3), para dejar la multiplicación así:
Simplificamos, eliminando el (x – 1) del numerador de la primera fracción y el (x – 1) del denominador de la segunda,
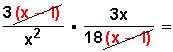
para quedar:
Simplificamos el resultado
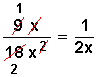
Y obtenemos el mismo resultado.
Este resultado es correcto para cualquier número que sea mayor que 1.
Ejemplo 2
Veamos el camino más corto:
Factorizamos donde es posible hacerlo (marcado en rojo):
Y simplificamos
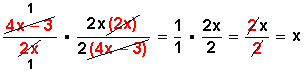
También pudimos hacerlo más largo:
Multiplicamos los numeradores entre sí y los denominadores entres sí
Factorizamos el resultado último y simplificamos:
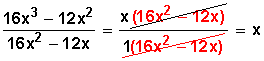
Ejemplo 3
Factorizamos lo que sea posible factorizar (en rojo):
Ahora podemos simplificar los términos semejantes que haya (en azul):
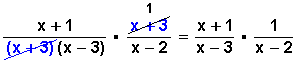
En seguida, multiplicamos numerador con numerador y denominador con denominador:
y como el (1) no se coloca, el resultado final queda
Generalmente se deja expresada la multiplicación, como en este caso del denominador, el cual queda factorizado.
Se debe anotar que este resultado solo es válido si x es distinto a 3, ya que si x = 3 tendríamos 3 -3 = cero, y sabemos que todo lo multiplicado por cero es igual a cero.
Ejemplo 4
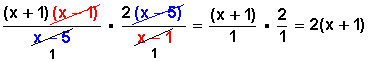
Hay que hacer notar que el resultado solo es posible siempre que x sea distinto a 1 y a 5.
¿Qué hicimos?
Factorizamos todo lo que se podía factorizar, simplificamos todo lo que se podía simplificar y multiplicamos numerador con numerador y denominador con denominador (este útimo da uno, que no se coloca).

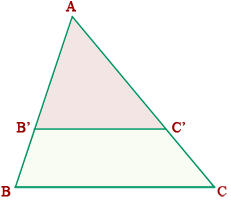

 .
.
![a^{\frac{n}{m}} = \sqrt[m]{a^n}](http://upload.wikimedia.org/math/3/9/8/3983643a5db08e21da69fffabbc0875c.png)
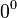 que, en principio, no está definido (ver
que, en principio, no está definido (ver 
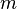 representa la
representa la 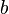 determina la
determina la  (llamado rectangular) no son consideradas lineales.
(llamado rectangular) no son consideradas lineales.
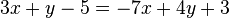


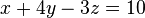
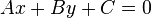

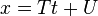


 y
y  . El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
. El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
 y
y  . El gráfico es una línea vertical, interceptando el eje X en E.
. El gráfico es una línea vertical, interceptando el eje X en E.
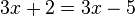 .
.